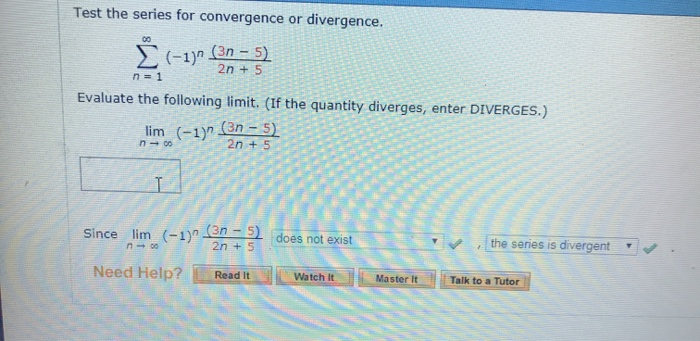
3n 5 N 1
Combine like terms on the left side.
3n 5 n 1. Number of times each prime factor appears in the factorization of:. You can put this solution on YOUR website!. (-3,-5) the length of rectangular table is 6 m more that its width and its area is 12 m² 2.
+ (2n-1)*(2n+1) = n(4n^2 + 6n - 1)/3 for all positive integer n. Simple and best practice solution for 3n-3=4n+1 equation. The sequence is converging if it has a.
Selecting "AUTO" in the variable box will make the calculator automatically solve for the first variable it sees. Start by adding the two equations together. 4 + 3n = 5 3n = 5 - 4 3n = 1 n = 1/3.
Just as in the last example, we guess that this is very much like the harmonic series and so diverges. 1 + 4 + 7 + :::. Check how easy it is, and learn it for the future.
Then, by the recursion step, n2Sand 1 2Simply n+ 1 2S. Therefore, the series X∞ n=1 en 3n−1 = e X∞ n=1 e 3 n−1 = e X∞ n=0 e 3 n, where the second equality comes from shifting the index by one. A)Show that the statement is true for any real number k.
A sequence is given by the formula un = 3n + 5, for n = 1, 2, 3,. You know that 12 inches = 1 foot. We know that jsinnj<1, so nsin2 n n3 + 1 n n3 + 1 n.
1+4+7+:::+(3n 2) = n(3n 1) 2 is true for all natural numbers n. (n + 1) (3n - 5) ——————— - ———————— = 0 3 6 Step 5 :. 1/n3^n Evaluate The Following Limit.
Free series convergence calculator - test infinite series for convergence step-by-step. )(* + , -. Formula of nth term in A.P is a+(n-1)d Where “a” is ist term and “d” is common difference according to qustion a+(n-1)d=3n+5 a+nd-d=3n+5 nd+(a-d) =3n+5 Compare this equation,we get d=3 & a-d=5 a-3=5 a=8 Seventh term= 8+(7–1)3 Ans will be 26.
In the quadratic equation 4x²+6x-3=0,which is the linear term 3) What are the roots of x2 = 8x - 15?A. =>3n (n-1)-5(n-1) 3.) factor out (n-1) from the. You can put this solution on YOUR website!.
(C) No, because it is not a p-series. Let’s note math(a/mathmath_n)_{n \in \mathbb N^*}/math the sequence. \Sigma_{n = 1}^\infty \frac{2n^2 + 3n}{\sqrt {5 + n^5}} By signing up, you'll get.
Sigma infinity n=1 n/n^4 + 1 4. The SEQUENCE (n-1)/(3n-1) converges on 1/3, as you noticed. Check how easy it is, and learn it for the future.
The sum of the first n terms S n of an arithmetic sequence is calculated by the following formula:. Learn more about BMC ›. Lim N → ∞ Bn 0 Since Lim N → ∞ Bn = 0 And Bn + 1 ≤ Bn For All N, The Series Is Convergent If The Series Is Convergent, Use The Alternating Series Estimation Theorem To Determine How Many Terms We Need To Add In Order To Find.
In an induction proof of the statement 4+7+10++(3n-1)=n(3n+5)/2 the first step is to show that the statement is true for some integers n. 3 (-1) -5 = -3 -5 = -8. S n = n(a 1 + a n)/2 = n2a 1 + (n - 1)d/2.
Suppose n2S, for some n 1. Notice that math\displaystyle 1 \times 3 \times 5 \times \ldots \times (2n-1)=\frac{1. Apply the distributive property by multiplying each term of n − 1 by each term of 3 n + 1.
New questions in Math. (a) Sigma infinity n = 1 n root 2 (b) sigma infinity n = 1 e^n/3^n - 1 (c) Sigma infinity n=1 ln(2n^2 + 1/3n^2 + 1) (d) sigma infinity n=1 1/1 + (2/3)^n (e) Sigma infinity n=2 1/n^2 - n (f) Sigma infinity n=1 ln(n/n + 1) 3. The ratio of m:n is 1:1/3 or 1/(1/3) or 3 Answer// 1 0.
If the nth term of a sequence is known, it is possible to work out any number in that sequence. Select the steps required to complete the proof. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor.
Ask Question + 100. 5 - x2 = 4x4. Explore many other math calculators, as well as hundreds of other calculators addressing health, fitness, finance, math, and more.
This time we apply the second principle of mathematical induction on nto show that if s2Sis produced by applying nsteps (1 initial. 3 h n + 4 h − (n − 1) (3 n + 1) Apply the distributive property by multiplying each term of n-1 by each term of 3n+1. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework.
N = -1 Write each equation in standard form.1. Join Yahoo Answers and get 100 points today. 1*3 + 3*5 + 5*7 +.
N=1 en 3n−1 is convergent or divergent. Using the nth term. Since n4 + 1 >n4, we have 1 n4+1 < 1 n4, so a n = n 2 n4 + 1 n n4 1 n2 therefore 0 <a n < 1 n2 Since the p-series P 1 n=1 1 2 converges, the comparison test tells us that the series P 1 n=1 n2 n4+1 converges also.
I think answer is 2 dear please follow me. "There are 7 more girls than boys in a club. 3n = 5 n = 1 2/3 As I said, the answer is supossedly not correct.
Add your answer and earn points. @ a.b c bed f , g6 h !" i j * k j l h3 m' n l o j * 3p. Now we show S N.
The sum of all these sequences will form a series. A n = a 1 + (n - 1)d. Get your answers by asking now.
How many girls are there in the club?" Let g represent the number of girls. Lelliggracee35 lelliggracee35 Step-by-step explanation:. (E) Yes, because of the term n 2 in the denominator.
N + 1 - 3n = -5 + n + 1 - 2 Combine like n - 3n = -2n -2n + 1 = -5 + n + 1 - 2 Combine like -5 + 1 - 2 = -6 -2n + 1 = n - 6 Subtract 'n' to both -3n + 1 = -6 Subtract 1 to both -3n = -7 Divide -3 to both n = 2 1/3 or 7/3. Solve for n 3n-5=-8(6+5n) Simplify. (B) No, as the terms of the series do not approach 0 as n →∞.
From core to cloud to edge, BMC delivers the software and services that enable nearly 10,000 global customers, including 84% of the Forbes Global 100, to thrive in their ongoing evolution to an Autonomous Digital Enterprise. We prove by induction that S n:. 1 = 1(3 1) 2 is true.
$\begingroup$ A lot of it is just keeping really good account of what is assumed in the inductive step and what is to be proved.Here you can see that we can assume the sum of the numbers up through $3n-2$ is $\frac{n(3n-1)}{2}$, and this fact is used in the very first equation. In this math video lesson on Multi-Step Equations I solve the equation 3n-5=-8(6+5n). Ex 4.1, 1 Important Not in Syllabus - CBSE Exams 21 Ex 4.1, 2 Not in Syllabus - CBSE Exams 21 Ex 4.1, 3 Important Not in Syllabus - CBSE Exams 21 Ex 4.1, 4 Not.
5.1 Find the Least Common Multiple The left denominator is :. 16.For which values of xdoes the series X1 n=0 (x 4)n 5n converge?. Thus, by the rst principle of mathematical induction, n2Sfor every natural number n 0.
Unfortunately, $${1\over\sqrt{n^2+3}} {1\over n},$$ so we can't compare the series directly to the harmonic series.A little thought leads us to $${1\over\sqrt{n^2+3}} > {1\over\sqrt{n^2+3n^2}} = {1\over2n},$$ so if. Do you have any ideas on how to solve it or where I've gone wrong?. B)Assume that the statement is true for some positive integer k.
Example 11.5.4 Does $\ds\sum_{n=1}^\infty {1\over\sqrt{n^2+3}}$ converge?. I can re-write the terms as en 3n−1 = e en−1 3n−1 = e e 3 n−1. X2 = 5x - 62.
Show that the statement is true for k+1. Add to both sides of the equation. 3x2 = 1 - 2x3.
Since e 3 < 1, we know that the geometric. The SERIES (n-1)/(3n-1) diverges. N!1 2n+ 3 n n4 (n2 + 3n+ 6)2 = 2 1 = 2:.
What is the sum of the series when it converges?. 3n + 5 = (n + n) +1/3. In a quadratic equation 4x2² - 4 = 0, which is the.
Next we prove by mathematical induction that for all natural numbers n, 1 + 4 + 7 + :::+ (3n 2) = n(3n 1) 2:. = (2-1)*(2+1) = 1*3 = 3. If it is convergent, find its sum.
Write the first five terms of the sequence \(3n + 4\). A sequence is a set of numbers defined by a function. When n = 1, we have:.
Since n2 < n2 +6n = n(n +6) for all n ≥ 0, we have 1 n(n +6) < 1 n2 Because P 1/n2 converges (it’s a p-series with p = 2 > 1), the comparison test implies that P 1/(n(n+6)) also converges. The sequence does converge, as you saw. Therefore, since the limit is nite and the series P n n4 = 1 n3 converges, the Limit Comparison Test implies that the given series converges as well.
Calculating the Least Common Multiple :. Start with the given equation. Use the integral Test to determine whether the series converges or diverges.
Let a n = n2=(n4 + 1). ∞ (−1)n N3n N = 1 Identify Bn. Tap for more steps.
Determine if the series is convergent or divergent. This video discusses how to solve an equation for a variable which is a. Add to both sides.
Comparison Tests (10.4) Does the series ∞ X n = 1 n n 2 + 3n + 5 1 / 2 converge?. If a=23×3,b=2×3×5,c=3n×5 and LCM (a, b, c) =23×32×5, then n = 1 See answer hariomsharmadms17 is waiting for your help. My True ValueEvaluate the following expressions for thes1.
Three less than the product of seven and a number is four more than the number. 7n − 3 = n + 4. All of Our Miniwebtools (Sorted by Name):.
There are 23 members in the club in all. 1 + 4 + 7. P 1 n=1 nsin2 3+1 Answer:.
An element divisible by $\,n.$. Tap for more steps. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework.
/-" $0 1 2 3 4 !. Assume that S k:. Strategy for Testing Series:.
$ all $ $ possible remainders mod $\,n.\,$ Therefore the sequence has an element with remainder $\,0,\,$ i.e. Tap for more steps. Simple and best practice solution for (n-3)(n-5)= equation.
Mark me as brainliest. 3 The right denominator is :. A SERIES is the sum of all the numbers in a sequence up to infinity.
Thus the remainders are the same as the base case $\ 0,1,2,\ldots,n-1\ =\:. \color{#C00}{a\,\equiv\, a\!+\!n}\pmod n,\:$ the shift does not change the remainders in the sequence. (A) No, since ∞ X n = 1 1 √.
6 7*8 " 9 1 $ :- ;=< > ?. Divide both sides by to isolate. (D) Yes, since ∞ X n = 1 1 √.
(n-1)(3n-5) 1.) write -8n as a sum or difference =>3n^2-3n-5n +5 2.) factor out 3n and -5 from the expression:. The statement S 1:. Related Answers solving equations by isolating variables and the square root principle Following all significant figure rules use your calculator to convert 9.7 feet to inches.
Est The Series For Convergence Or Divergence. Our PWA (Progressive Web App) Tools (17) {{title}} Financial Calcuators (121). Add to both sides.
+ (3k 2) = k(3k 1) 2 is true and prove that S k+1:. Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations −n+(−3)+3n+5 so that you understand better. I think they meant that the SERIES diverges;.
Combine like terms on the right side. This free number sequence calculator can determine the terms (as well as the sum of all terms) of an arithmetic, geometric, or Fibonacci sequence. Apply the distributive property.
P 1 n=1 n2 4+1 Answer:. Since (−5)−n = (−1/5)n, this is a geometric series.Because |−1/5| < 1, it converges.

2 Prove That 1 3n 4n For All N 1 5 Marks Homeworklib
N Is An Integer Such That 3n 2 14 And 6n N 2 5 1 What Are All Values For N Quora

Ncert Solutions For Class 11 Maths Chapter 9 Sequences And Series Ecuaciones
3n 5 N 1 のギャラリー
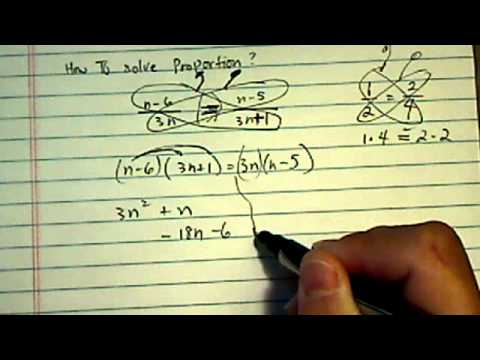
Shortcut To Solve Proportion N 6 3n N 5 3n 1 Youtube

Ex 4 1 10 Prove 1 2 5 1 5 8 1 8 11 1 3n 1 3n 2

Hhh

Math 319 Problem Set 3 Solution 21 February Pdf Free Download

Solved Test The Series For Convergence Or Divergence 1 Chegg Com
2

Wolfram Alpha Examples Step By Step Solutions
2

Factoring Trinomials Bingo Card
3n2 5n 6 8n2 3n 2

Add And Subtract Polynomials Practice

Prove Using Mathematical Induction That 2 3n 3 N Is Divisible By 5 For All N 1 Mathematics Stack Exchange
Solved Math 401 Introduction To Analysis I Spring Term 18 Problems 11 Return By Monday 2nd April 1 Prove That If Gt D And An Is A Sequen Course Hero
2

Answered Define The Double Factorial Of N Bartleby
Q Tbn 3aand9gcrbsa3mqasj3qwxo0tft8ga7ij4hotf Xtegee3 U2atv2r5 Cd Usqp Cau

Mathematical Induction Prove That 3 5 2 N 1 2 3 N 1 Is Divisible By 17 Youtube

Solved Test The Series For Convergence Or Divergence 00 Chegg Com
2
2

Parrc Test Practice Question 4 For Algebra 1 Belle Chasse High School

40 3n High Resolution Stock Photography And Images Alamy
2
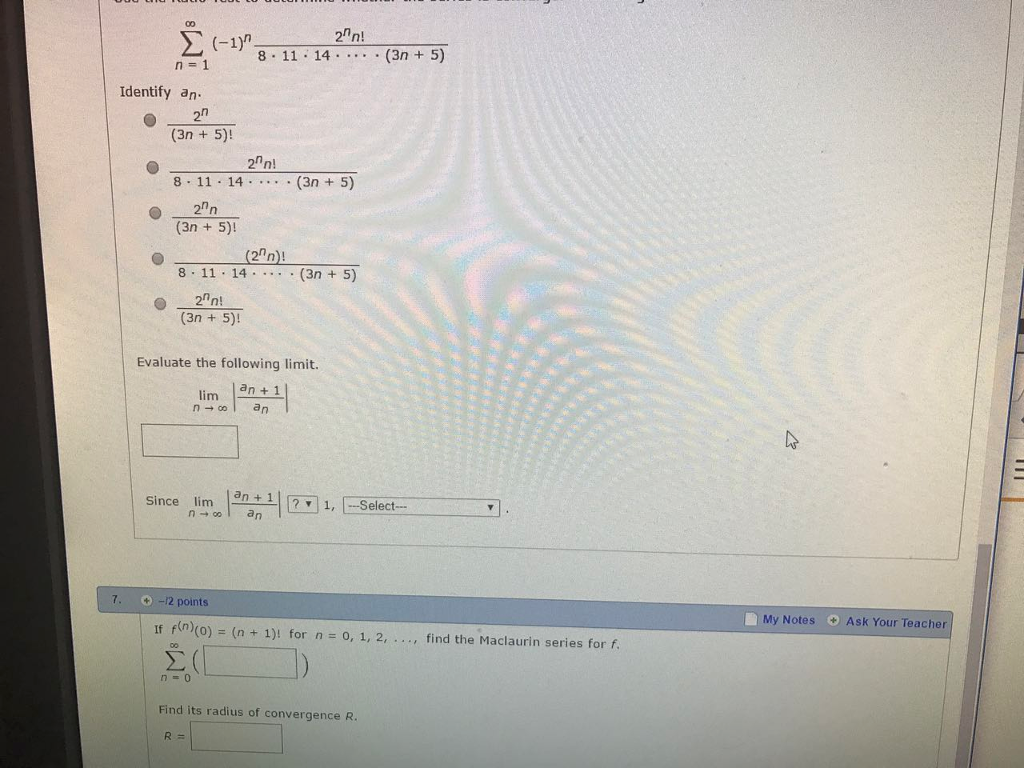
Solved Sigma Infinity N 1 1 N 2 N N 8 Middot 11 Mid Chegg Com
2
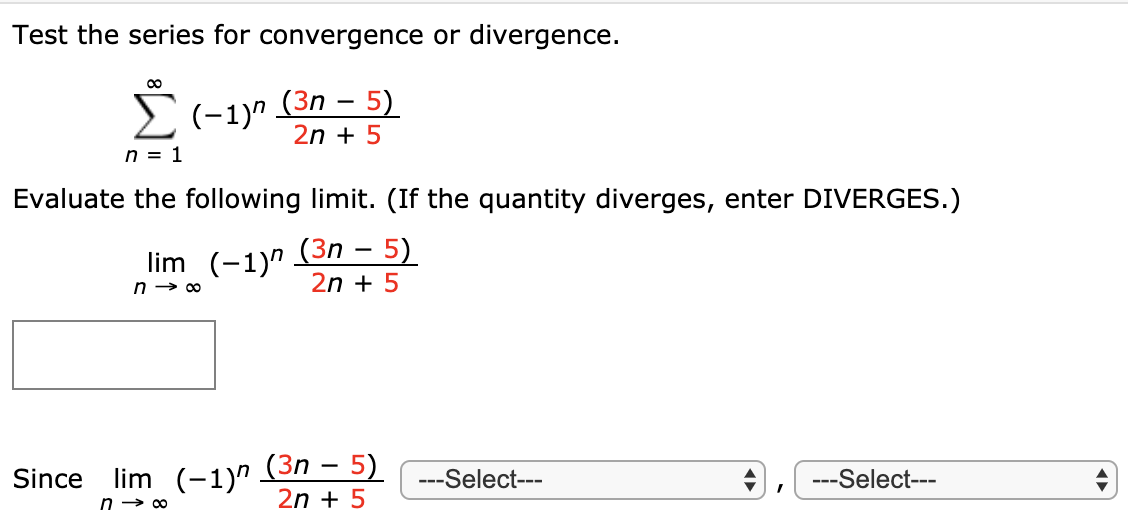
Solved Test The Series For Convergence Or Divergence An Chegg Com
Http Www Lyndhurstschools Net Userfiles 318 Classes Doc Pdf Id

Solved Problem 10 Consider The Following Series 2 3n Chegg Com

Answered Properties Of Exponents Simplify Bartleby

Convergent Divergent Geometric Series With Manipulation Video Khan Academy

Solved Example 1 Determine Whether The Series S 3 2n2 3 Chegg Com
2
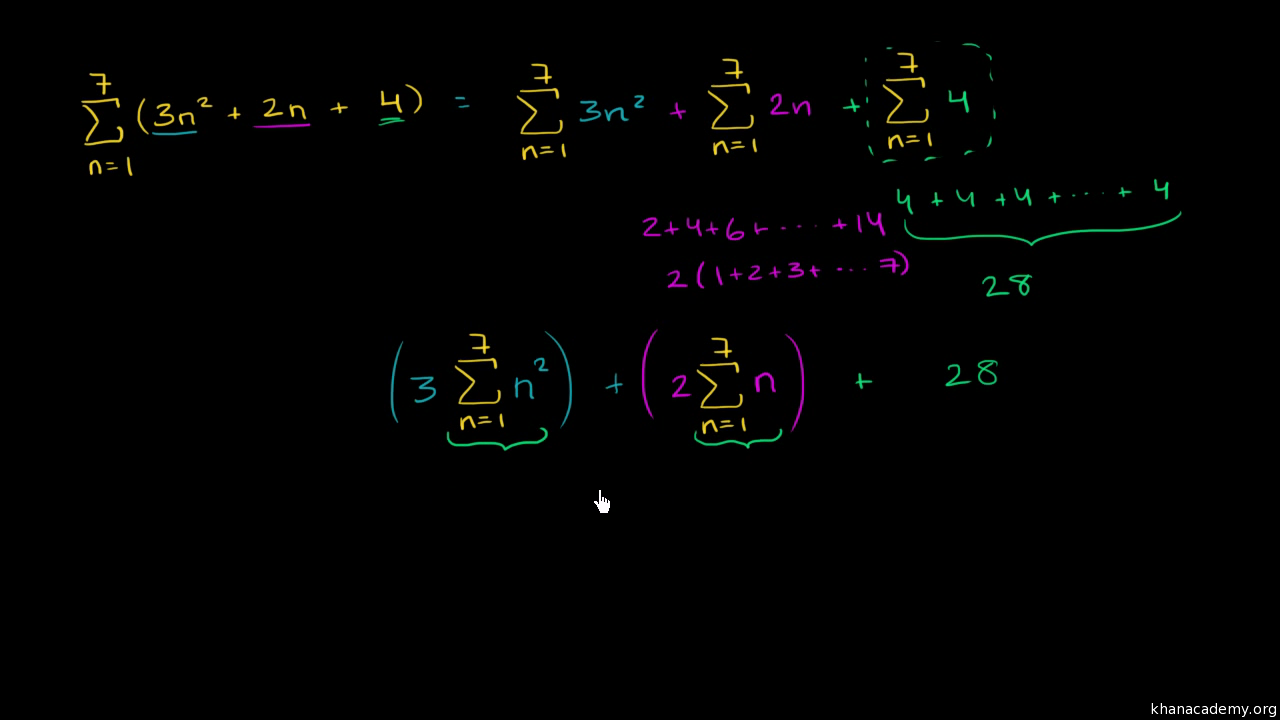
Evaluating Series Using The Formula For The Sum Of N Squares Video Khan Academy
2

1 3 N 1 2 1 6 3n 5 For N Brainly In
2

Solved Use The Binomial Series To Expand The Function As Chegg Com

Warm Up Simplify Using Only Positive Exponents 1 7n 2 3n 5 2 4y 6 3 Solve For The Value Of X Ppt Download

10 2 Practice Operations On Functions Perform The Indicated Operations Copyright Law Media Freedom

A Specular X Ray Diffraction Spectra Of Ba 2 Ma N 1 Pb N I 3n 1 Download Scientific Diagram
Find The Sum Of Series 3 7 13 21 31 Geeksforgeeks

Using Mathematical Induction To Prove 2 3n 3 N Is Divisible By 5 Youtube

40 3n High Resolution Stock Photography And Images Alamy
View Question Help

5n 1 3n 1 Problem Smallest Repeating Cycle And Collatz Conjecture Mathematics Stack Exchange

1 A Quadratic Equation Is An Equation Equivalent To One Of The Form Where A B And C Are Real Numbers And A 0 To Solve A Quadratic Equation We Get Ppt Download
2
Teachingcenter Ufl Edu Files Exam 2 Review Problems Mac 2312 Pdf
2

Solved Sigma N 1 To Infinity 3n 5 N 2 1 2 Sigma Chegg Com
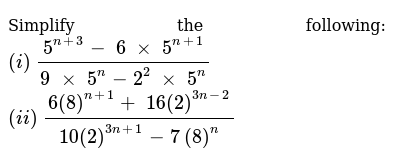
Simplify The Following I 5 N 3 6 Xx 5 N 1 9 Xx 5
2
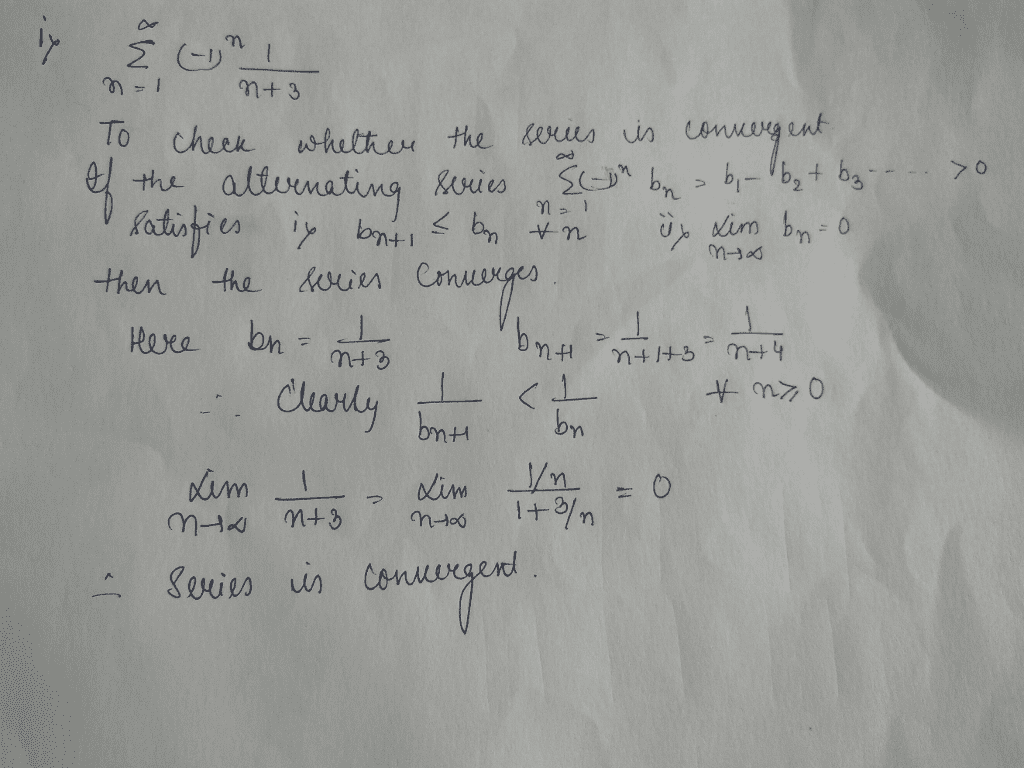
Oneclass 4 Alternating Series Questions Aoe Net 272 N N 1 I 1 N 1 22n 5 3n N 5 N 1 1 3

Answered Prove Vn E Z If N Is Odd Then 3n 5 Is Bartleby

Show That 1x2 2 2 X 3 2 N N 1 2 1 2 X 2 2 2x3 N 2 N 1 Math Meritnation Com
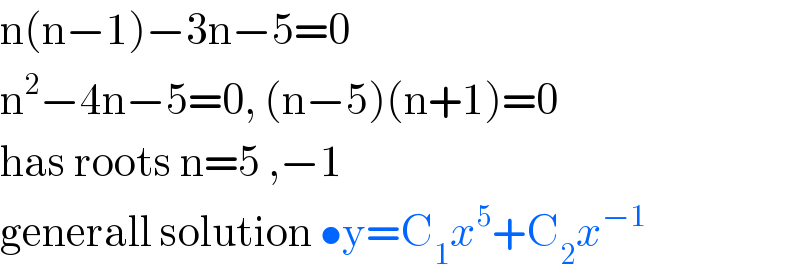
Tinkutara Equation Editor Math Forum Question
If Math S N 3n 2 2n Math Is The Sum Of First Math N Math Terms Of Arithmetic Progression How Do You Find The Second Term Of The Sequence Quora
2

Grade 9 Mathematics Arithmetic Progressions I Don T Know But This Method Of Solving Seems Suspicious To Me Even Though The Answer Is Correct I Suspect There Must Be Some Other Way

Module 1 Simultenous Linear And Equations
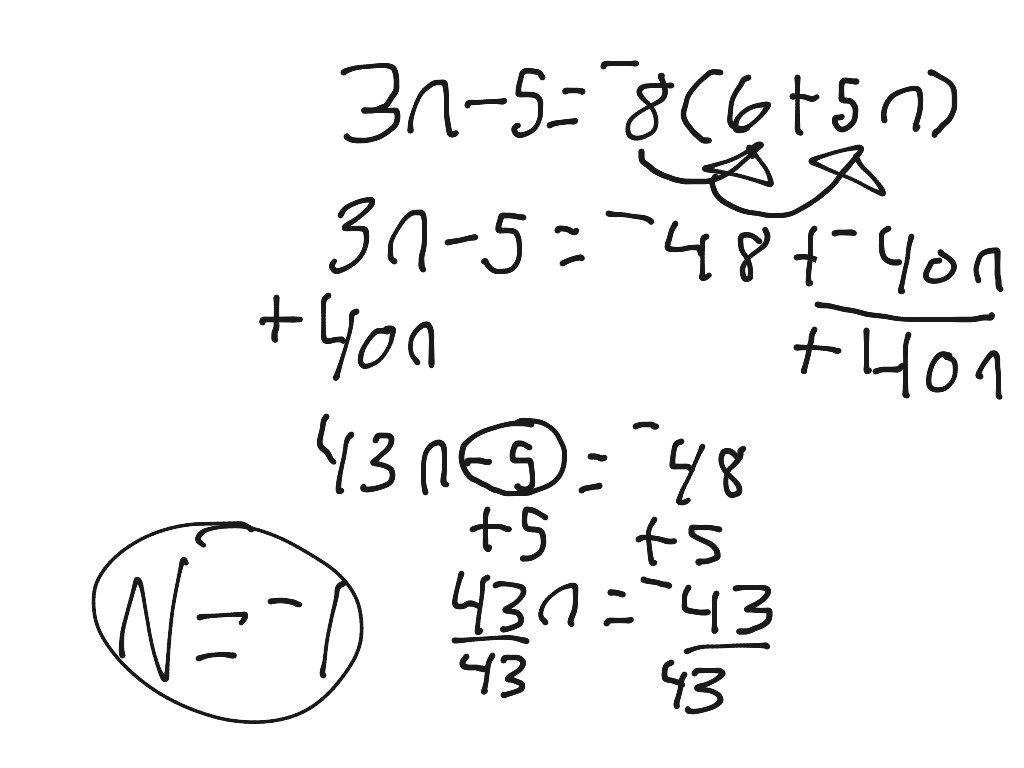
Autumn Wellons Showme
2

Simplify The Following M N 2m 3n Brainly In

Solve 3p N 4 P N 1 5 Factorial Permutation Equation Youtube

Find All Integers N Such That Square Root Of 3n 5 N 1 Is Also An Integer Math Real Numbers Meritnation Com

Question 4 Javascript Chapter 4 5 25 Points N Homeworklib

Ppt 1 2x 4 12 2 3n 5 3 2n 4 3 6x 5 5x 4x 5 X 2 4 7 4x 1 14 0 5 2x Powerpoint Presentation Id

Document

Solving Equations With Variables On Both Sides Quiz Quizizz
Http Www Lcps Org Cms Lib4 Va Centricity Domain Unit 1 day 1 one variable eqns hw key Pdf

Solved I M Really Having Trouble Understanding How To Get Chegg Com

Prove That The Sequence N 2 3n 5 2n 2 5n 7 Converges To

Ppt Solve Graph Powerpoint Presentation Free Download Id

ลำด บและอน กรม

3 27 N 1 9 3 3n 1 8 3 3n 5 27 N Simplify Brainly In

Solved Determine Lim X Rightarrow Infinity 2 N 3 4 N 5 Chegg Com

Module 1 Simultenous Linear And Equations
Http Www Standardsinstitutes Org Sites Default Files Material Summer18 Math Leadership I 6 8 Facilitator Resource Pdf
Http Www Cobblearning Net Poole1 Files 16 01 Day 2 Factoring Review W Key Rgvgne Pdf

32 Uidoubled D Tripled 25 Which Of The Following Groups Of Forces Could Be In Equilibrium
Q Tbn 3aand9gcsklspyjhc5bbupnat Vxgdz9h8ogfxdmgq0dxpvlvtszciuuad Usqp Cau
2

Algebra 2 Section 4 4 Part 2 24 Minutes Yankton High School

Describe The Domain Of Each Function Or Sequence Below A The Function F X 3x 5 B The Sequence T N 3n 5 C The Function F X Frac 5 X D The Sequence T N Frac
Http Canonmac Pbworks Com W File Fetch Quadratic equation word problems teacher notes 4 1 15 Pdf
Http Www Cobblearning Net Poole1 Files 16 01 Day 2 Factoring Review W Key Rgvgne Pdf

What Is The Limit Of The Infinite Series 3n 5 4n 5 1 N 1 Enter Your Answer In The Box Enter Brainly Com

A Crystal Structures Of The R N 1 Co 3n 5 B 2n Compounds N 0 And Download Scientific Diagram

Solving Equations With Variables On Both Sides Quiz Quizizz

New Industar 61 L D Lens E Mount Sony Nex 3 C3 F3 3n 5 N 5r 5t 6 A 7 7r 7s Ebay

Final 16 Questions And Answers Mat 132 Calculus Ii Studocu
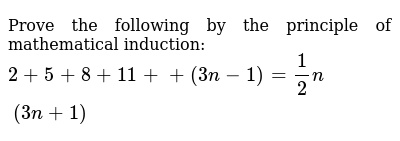
Which Equation Has The Solution N 1 1 Answer Choices 3n 5 1 7

If N Is Odd Then 3n 7 Is Even Pdf Free Download

Ex 9 4 6 Find Sum 3 X 8 6 X 11 9 X 14 Chapter 9 Class 11
2

5n 1 3n 1 Problem Smallest Repeating Cycle And Collatz Conjecture Mathematics Stack Exchange

Solve 3p N 4 P N 1 5 Factorial Permutation Equation Youtube

Solutions To Midterm 1 Question 1 Recurrence Relation T N 4t N 2 N 2 N 2 T 1 1 A Height Of The Recursion Tree Assume N 2 K Height K Ppt Download

8 8 3n 5 N 1 4n 1 8 I Need Help On The Steps Brainly Com



