24n+3 + 33n+1 Habis Dibagi 11
Terlihat bahwa semua bilangan genap n (4 ≤ x ≤ ) dapat dinyatakan sebagai penjumlahan 2 bilangan prima.

24n+3 + 33n+1 habis dibagi 11. N 2 – 4n – 3 = 0. N-4n^2 habis dibagi 3 untuk semua n bilangan bulat, n>atau samadengan 2!. Jumlah 9 suku pertama sama dengan 225 dan suku yang ke-7 adalah 38.
Ganjil antara 300 dan 700 b. Misalkan n adalah bilangan lima angka dan m adalah bilangan empat angka yang. N 2 – 4n – 3 = 0.
Tentukan jumlah seluruh angka yang terdiri dari dua angka dan habis dibagi dengan 3 Jawab :. Antara 100 dan 1000 yang habis dibagi 4 atau 10 8. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11.
Barisan geometri Barisan geometri memiliki ciri, perbandingan antara dua suku yang berurutan selalu tetap. Jadi, kita dapat menyimpulkan bahwa 5 n – 1 habis dibagi 4 untuk semua bilangan bulat positif n. Untuk n = 11k + 10 maka n2 + 2n + 12 = 121k2 + 242k + 132 = 121 (k2 + 2k + 1) + 11 maka :.
Diket ahui deret aritmatika 7 + 10 +13 + 16 + 19 + …. 12 + 15 + 18 + 21 + 24 + 27 + 30 + 33 + 36 + 39 + 42 + 45 + 48 + 51 + 54 + 57 +. Suku ke 12 a + 11b = 42.
Yang akan dibuktikan di sini adalah kaidah B 1. Terletak antara 1 dan 150 yang habis dibagi 3 tetapi tidak habis dibagi 5 B. Maka, deret yaitu 1+2+3+4+5.
An - bn habis dibagi a - b untuk n bilangan asli. Ditentukan bilangan aasli kurang dari 50. Diketahui deret aritmatika U 2 +U 3 =12 dan U 7 =15.
Berapa banyaknya pengunjung pada hari ke-12 jika mengalami kenaikan tetap?. 2 = Jika n bulat maka n 2 – 2 – 4n = 1. Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube.
N + 13 habis dibagi 7 Berapakah sisanya jika n dibagi 31?. Contoh Soal Barisan dan Deret Aritmatika Geometri, Pengertian, Rumus, Sifat-sifat Notasi Sigma, Tak Hingga, Hitung Keuangan, Bunga Tunggal Majemuk Anuitas, Matematika - Pernahkah kalian mengamati lingkungan sekitar?. Antara 52 dan 150 yang habis dibagi 5.
Carilah suku pertama, kedua, dan suku terakhir. D) 5 di dalam Z13 :. Terbukti bahwa n2 + 2n + 12 bukan merupakan kelipatan 121.
4 3 2 Jika a = 1,333 dan b = 1,777, maka blog a = … 3 2 1 Hasil kali dari penyelesaian persamaan :. 2 = Jika n bulat maka n 2 – 2 – 4n = 1 Dengan cara yang sama didapat bahwa n 2 – 2. Karena k 3 -k habis dibagi 3, maka k 3 -k mempunyai factor 3, sehingga k 3 -k dapat dinyatakan dengan 3t.
Hanya bentuk 11k + 10 saja yang membuat n2 + 2n + 1 habis dibagi 11. British Mathematical Olympiad 00 Round 1) Solusi :. Bilangan habis dibagi kurang dari 150 habis dibagi 3 :.
Deret tak hingga adalah suatu deret yang banyak. Antara dan 100 yang habis dibagi 3. $5 \equiv 2 \pmod 3$ karena $5-2$ habis dibagi $3$.
Antara 52 dan 150 yang habis dibagi 5. Dengan cara yang sama didapat bahwa n 2 – 2. N 2 – 4n – 3 = 0 n 1.
Hanya bentuk 11k + 10 saja yang membuat n2 + 2n + 1 habis dibagi 11. Barisan dan Deret Geometri Barisan Geometri Adalah suatu barisan dimana perbandingan dua suku yang berurutan selalu sama ( tetap ). Kita ingin membuktikan bahwa setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima.
Garis y = x melewati titik (0, 0). $10 \equiv 0 \pmod 5$ karena $10-0$ habis dibagi $5$. (64 – 2n) b.
Antara dan 100 yang habis dibagi 3. ∙ b, dengan mengambil b yang sekecil –kecilnya. Kita anggap 5 k – 1 habis dibagi 4 untuk sebarang bilangan bulat positif k.
Jumlah bilangan bulat antara 10 dan 60 yang habis dibagi 3 adalah 17. Antara 0 dan 500 yang habis dibagi 4 d. 5.Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 2 4n+3 +3 3n+1 habis dibagi oleh 11.
9 11.Misalkan l merupakan banyaknya pasangan bilangan bulat (m;n) sehingga mn = 28m+ n2. Misalnya, sungguh sulit kita merumuskan pola bilangan-bilangan 5, 7, 11, 17, 25 secara singkat dengan kata-kata. 12 10.Misalkan N merupakan bilangan asli terbesar yang memenuhi syarat habis dibagi 36, semua digitnya genap, dan tidak ada dua digit yang sama.
(66 – 2n) e. Genap antara 300 dan 700 c. Menyelesaikan masalah-masalah yang berkait.
Antara 52 dan 150 yang habis dibagi 5. Suatu barisan aritmatika diketahui suku ke – 12 adalah 42 dan suku ke – adalah 26. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11.
Simplenya, 1, 2, 3, 4, 5 adalah barisan. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11. (k 3 -k)+3 k 2 +k =3t+3 k 2 +k mempunyai factor 3.
2 = Jika n bulat maka n 2 – 2 – 4n = 1. Antara 52 dan 150 yang habis dibagi 5. N2 + 2n + 12 jika dibagi 121 bersisa 11.
Un = 14 + 11 x ½. Faktur adalah bukti pembelian atau penjualan barang secara. N 2 – 4n – 3 = 0.
Belajar Induksi Matematika dengan video dan kuis interaktif. Berapakah banyaknya bilangan asli kurang dari 0 yang habis dibagi 3 ?. (72 – 2n) d.
Di sekeliling kalian tentulah banyak terjadi hal-hal yang bersifat rutin. Yang akan dibuktikan di sini adalah kaidah B 1. N + 11 habis dibagi 13 iii.
Misalkan n adalah bilangan lima angka dan m adalah bilangan empat angka yang. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11. N 2 – 4n – 3 = 0 n 1.
Antara dan 100 yang habis dibagi 3. Notasi sigma merupakan simbol yang dipakai untuk menyingkat penjumlahan sejumlah bilangan yang berpola tertentu. Sudut lancip adalah suatu sudut yang besarnya 900 atau Candi Borobudur terletak di Jawa Tengah.
Deret adalah penjumlahan dari suatu barisan. 93 adalah bilangan prima. 10 Karena banyaknya faktor adalah 11 dan juga 32 1 dapat dibagi oleh , maka n = 11 + 1 = 12.
50 adalah habis dibagi 5 atau 3. Berapakah banyaknya bilangan asli antara 10 dan 85 yang habis dibagi 5 ?. Pernyataan ini diasumsikan benr, maka akan dibuktikan pada urutan berikutnya yaitu n= k+2.
Dan 10 habis dibagi 10. Pembuktian kaidah B 2 dan B 3 diserahkan kepada pembaca. Carilah rumus umum dari 1^3 =1, 2^3 = 3 + 5, 3^3 = 7+9+11, 4^3 = 13 +15 + 17 + 19 Kemudian buktikan dengan induksi matematika.
51 habis dibagi 3. Un = 19 ½ (E) 4. Rumus suku ke (n - 2) adalah….
Tentukan jumlah semua bilangan bulat :. Dengan cara yang sama didapat bahwa n 2 – 2. Bilangan bulat positif disebut prima jika dan hanya jika bilangan bulat tersebut habis dibagi dengan 1 dan dirinya sendiri.
1 x 1 2n tidak habis dibagi oleh x 2 x 1 jika n 33. Carilah suku pertama, kedua, dan suku terakhir. Soal 2.5.4 Tentukan invers dari a) 2 di dalam Z11 ;.
Misalnya, sungguh sulit kita merumuskan pola bilangan-bilangan 5, 7, 11, 17, 25 secara singkat dengan kata-kata. Dimana x menyatakan bilangan bulat yang kurang dari atau sama dengan x. 3) n = k+2, 3 n +7 n =3 k+2-+7 k+2 = 9.3 k +49.7 k angka koefisien terbesar adalah 49, maka untuk 3 k, juga harus berkoefeisen 49.
$143$ habis dibagi $11$ karena $(1 + 3) - 4 = 0$ habis dibagi $11$. 2) n = k, 3 k +7 k habis dibagi 10 = 10 a. Maka nilai 2a + b adalah?.
2 = Jika n bulat maka n 2 – 2 – 4n = 1. Jumlah 9 suku pertama sama dengan 225 dan suku yang ke-7 adalah 38. Jumlah bilangan bulat antara 50 dan 100 yang habis dibagi 3 tetapi tidak habis dibagi 5 adalah … 150 1150 1050 1225 1275 Suku ke-4 deret geometri = 64 dan suku ke-7 = 512, maka rasio = ….
Metode pembuktian ini digunakan untuk membuktikan pernyataan yang bergantung pada bilangan bulat positif. Oleh karenanya pola bilangan dapat dirumuskan dengan cara-cara lain. Oleh karenanya pola bilangan dapat dirumuskan dengan cara-cara lain.
Karena 4 ∙ 5 k dan 5 k – 1 habis dibagi 4 maka 5 k + 1 – 1 habis dibagi 4. Tentukan suku ke 35 dari barisan tersebut 7. 5.3 Teorema Fermat dan Teorema Euler Untuk sembarang bilangan bulat positif m dinotasikan ' (m) sebagai banyaknya bilangan bulat positif yang kurang dari m dan.
N + 7 habis dibagi 11 ii. Rumus suku ke n Jumlah suku pertama Jawab :. Antara dan 100 yang habis dibagi 3.
Sisa N dibagi 28 adalah :::. Jumlah bilangan bulat dari 5 sampai 25 yang tidak habis dibagi 4 adalah 18. Pada pembahasan ini kita akan berlatih untuk membuktikan suatu pernyataan matematis dengan menggunakan induksi matematika.
3log2x – 2 3log x – 3 = 0, sama dengan …. Prinsip Induksi Matematika Untuk setiap bilangan bulat positif n, misalkan P(n) adalah pernyataan yang bergantung pada n. N2 + 2n + 12 jika dibagi 121 bersisa 11.
Simbol sigma yang dimaksud adalah $\displaystyle \sum$, yang dalam bahasa Inggris dikenal sebagai summation (disingkat “sum“), biasa kita menyebutnya dengan sumasi.Notasi sigma mulai diperkenalkan penggunaannya saat siswa mempelajari materi mengenai barisan dan deret serta. Misalnya, sungguh sulit kita merumuskan pola bilangan-bilangan 5, 7, 11, 17, 25 secara singkat dengan kata-kata. Yang sangat jelas habis dibagi 4.
C) 7 di dalam Z16 ;. March 11, 19 Pembahasan mata pelajaran matematika kali ini akan mengupas persoalan mengenai barisan dan deret aritmatika. Rumus suku ke n Un= bn + a - b = 3n + 4 - 3 = 3n + 1 Jumlah suku pertama S = 1 n (a + Un) 2 = 1.
121n - (-4)n habis dibagi 125 1900n - 25n habis dibagi 1875 sedangkan 125.1875 maka 125.1900n - 25n 121n - 25n + 1900n - (-4)n habis dibagi 125 121n - 25n habis dibagi 96 sedangkan 16 membagi 96. Terletak antara 100 dan 500 yang habis dibagi 6 c. Jumlah 9 suku pertama sama dengan 225 dan suku yang ke-7 adalah 38.
Pengunjung salon HAPPY hari pertama 25 orang, hari ke-2 30 orang. (4 + 61) 2 = 650 3. Karena itu, dari persamaan terakhir dapat dilihat bahwa setiap faktor dapat dibagi oleh 2.
Maka jumlah 5 suku pertamanya adalah…. 14=3+11 16=5+11 18=7+11 =7+13. Bilangan habis dibagi $11$ jika dan hanya jika selisih dari jumlah digit - digit pada posisi genap dengan jumlah digit - digit dari posisi ganjil habis dibagi $11$ Contoh :.
Untuk n = 11k + 10 maka n2 + 2n + 12 = 121k2 + 242k + 132 = 121 (k2 + 2k + 1) + 11 maka :. Tentukan nilai dari r. Oleh karenanya pola bilangan dapat dirumuskan dengan cara-cara lain.
Basis induksi untuk membuktikan bahwa 3n + 3 < n 2 + 3n adalah. Suku tengah deret itu adalah A. Akan kita tunjukkan 5 k + 1 – 1 juga habis dibagi 4.
Antara dan 100 yang habis dibagi 3. N 2 – 4n – 3 = 0. Carilah banyaknya bilangan dari barisan tersebut yang habis dibagi 3!.
Jumlah 9 suku pertama sama dengan 225 dan suku yang ke-7 adalah 38. Dengan cara yang sama didapat bahwa n 2 – 2. (70 – 2n) Penyelesaian:.
4.Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 72n+1 +1 habis dibagi oleh 8. B) 7 di dalam Z15 ;. Yang akan dibuktikan di sini adalah kaidah B 1.
Yang akan dibuktikan di sini adalah kaidah B 1. Akar dari x2 = 4 adalah 4 atau â¬4. Berapakah banyaknya bilangan asli antara 100 dan 300 yang habis dibagi 8 tetapi tidak habis dibagi 12 ?.
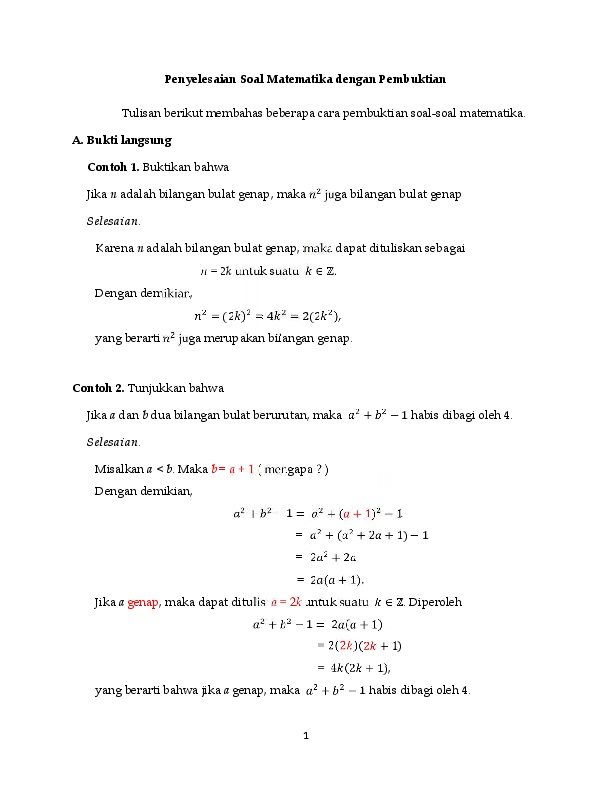
Metode Pengecekan secara umum Buktikan bahwa jumlah 2 bilangan genap adalah genap. Persoalan yang paling sering muncul atau ditanyakan adalah mencari suku ke-n dari suatu barisan, menentukan beda antar suku, menentukan banyaknya suku dan mencari nilai suku pertama. (AHSME/1980) Untuk suatu bilangan real r, polinom 8x 3 4x 2 42x 45 habis dibagi oleh x r 2.
Kisah Saya dan Matematika. Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11. Antara 52 dan 150 yang habis dibagi 5.
Carilah banyaknya bilangan dari barisan tersebut yang habis dibagi 3!. Jadi persamaan bisa dbentuk menjadi,. Antara 100 dan 1000 yang habis dibagi 4 dan 10 f.
Yang akan dibuktikan di sini adalah kaidah B 1. Soal 2.5.5 Gunakan Prosedur 7 untuk menentukan invers dari. 3, 6, 9, 12, …, 147 b = 3 a = 3 Un = 147.
Antara 0 dan 500 yang tidak habis dibagi 4 e. Yang akan dibuktikan di sini adalah kaidah B 1. 8 adalah bilangan ganjil atau delapan habis dibagi lima.
Dan gunakan hasil ini untuk memeriksa apakah habis dibagi 11:. (AHSME/1980) Polinom x sama dengan. $12 \equiv 1 \pmod {11}$ karena $12-1$ habis dibagi $11$.
Dapatkan pelajaran, soal & rumus Induksi Matematika lengkap di Wardaya College. Terletak antara 10 dan 40 yang habis dibagi 3 b. 2 = Jika n bulat maka n 2 – 2 – 4n = 1 Dengan cara yang sama didapat bahwa n 2 – 2.
Bilangan a habis dibagi 11 jika jumlah silang tanda ganti angka-angkanya (a n – a n-1 + a n-2 + … ) habis dibagi 11. (68 – 2n) c. Terbukti bahwa n2 + 2n + 12 bukan merupakan kelipatan 121.

Teori Bilangan

Induksi Matematika

Pengertian Bilangan Ganjil Dan Genap Serta Contohnya Advernesia
24n+3 + 33n+1 Habis Dibagi 11 のギャラリー

Buktikan N N Habis Dibagi 3 Untuk Setiap N Bilangan Asli Brainly Co Id

Teori Bilangan

Soal Latihan Induksi Matematika
Induksi Matematika Materi Lengkap Matematika

Mohammad Irfan Yulfa Matematika Informatika 3

Induksi Matematika Nelly Indriani Widiastuti Teknik Informatika Unikom Ppt Download

Source Code Listing Angka Yang Habis Dibagi 3 Atau 7 Menggunakan Bahasa Pemrograman Java Ketikan Md

Modul 1 Bilangan Bulat
Induksi Matematika Materi Lengkap Matematika

Buktikan Dengan Induksi Matematika Bahwa 5 N 1 Habis Dibagi 4 Untuk Semua Bilangan Positif N Brainly Co Id

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Soal Jawab Induksi Matematika Habis Dibagi 3 Youtube

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Materi Contoh Soal Dan Pembahasan Olimpiade

Induksi Matematika Matematika

Kunci Silabus Rpp Pr Matematika 11a Wajib Edisi 19 Pdf Matematika Kelas Xi Semester 1 I 1 Peserta Didik Mampu Menjelaskan Konsep Notasi Sigma Course Hero

3 N 1 Habis Dibagi 8 Brainly Co Id

Soal Latihan Uts Kelas Xi Matematika Wajib

Kumpulan Rumus Matematika Flip Book Pages 251 280 Pubhtml5

Lembar Aktivitas Siswa Matematika15 A Notasi Sigma 1 Pengertian Notasi Sigma Misalkan Jumlah Pdf Document

Modul Logika Matematika

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Ciri Bilangan Habis Dibagi Tiga

Fakultas Sains Dan Teknologi Ppt Download

Matematika Wajib Kelas Xi Ips

Buktikan Bahwa 3 N 1 Habis Dibagi 8 Untuk Semua Bilangan Bulat Positif N Brainly Co Id
Buktikan Bahwa 5 3n 1 1 Habis Dibagi 24 Brainly Co Id

2 Soal Dan Pembahasan Induksi Matematika Nomer 6 Youtube
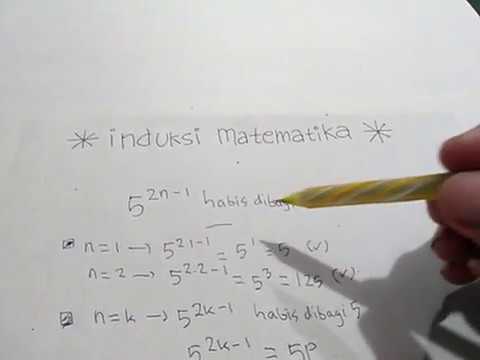
Soal Jawab Induksi Matematika Habis Dibagi 5 Youtube

Dengan Induksi Mtk Tunjukkan Bahwa 5 N 3n 1 Habis Dibagi 9 Untuk N Bilangan Asli Brainly Co Id

Induksi Matematika Nelly Indriani Widiastuti Teknik Informatika Unikom Ppt Download

9n 1 Habis Dibagi 8 Mas Dayat

Bab I Induksi Matematik Induksi Matematik Merupakan Salah

Soal Jawab Induksi Matematika Habis Dibagi 7 Youtube
Induksi Matematika Materi Lengkap Matematika

Pdf Soal Soal Olimpiade Matematika Dan Penyelesaiannya Ary Brainer Academia Edu

Bank Soal Olimpiade Matematika

Contoh Soal Induksi Matematika Dan Jawaban Pembahasan

Induksi Matematikabuktikan6 7 N 2 3 N Habis Dibagi 4 Brainly Co Id

Induksi Matematika Makalah Prinsip Dan Contoh Soal

Induksi Matematika Pembuktian Pernyataan Habis Dibagi Belajar Mat
Jejakseribupena Files Wordpress Com 16 10 Logika 7 Soal Pdf
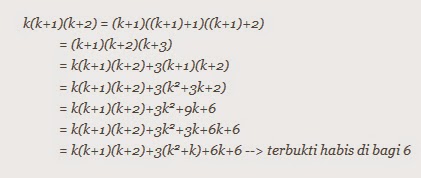
Buktikan N N 1 N 2 Habis Dibagi 6 Matematika Sup 2 Sup

Prinsip Induksi Matematika

Buktikan Dengan Induksi Matematika Bahwa 2 Pangkat 2n 1 1 Habis Dibagi 3 Brainly Co Id
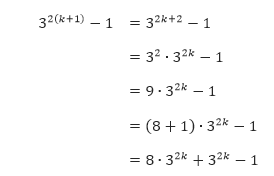
25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Doc Kumpulan Soal Jawab Olimpiade Matematikadaripertemuan Berau Putri Utiw Academia Edu

Bank Soal Olimpiade Matematika

Induksi Matematika Pembuktian Pernyataan Habis Dibagi Belajar Mat

Induksi Matematika Pembuktian Pernyataan Habis Dibagi Belajar Mat

Ciri Ciri Bilangan Habis Dibagi Defantri Com

Modul 1 Bilangan Bulat

Soal Pembinaan Olimpiade Mtk Sma By Hudah Riyanto Issuu

Logika Matematika Bab 5 Induksi Matematika Ppt Download
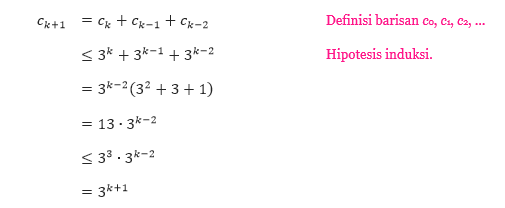
25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 6

Matematika Wajib Kelas Xi Ips

25 Soal Dan Pembahasan Induksi Matematika

Induksi Matematika Pembuktian Deret Keterbagian Pertidaksamaan

Soal Latihan Induksi Matematika

9n 1 Habis Dibagi 8 Mas Dayat

Kelas 11 Sma Matematika Siswa 17 Pages 1 50 Text Version Anyflip

Induksi Matematika Ppt Download

Buktikan Bahwa N Pangkat 3 N Habis Dibagi 3 N Lebih Besar Sama Dengan 2 Youtube

Bank Soal Dan Pembahasan Matematika Dasar Sukubanyak Polinomial 62 Defantri Com

Logika Matematika Bab 5 Induksi Matematika Ppt Download

Bab I Induksi Matematika 2 Buktikan Bahwa N3 5n Dapat Dibagi Dengan 6 Untuk Semua N N 3 Buktikan Pdf Document

Soal Induksi

2 Soal Dan Pembahasan Induksi Matematika Nomer 6 Youtube
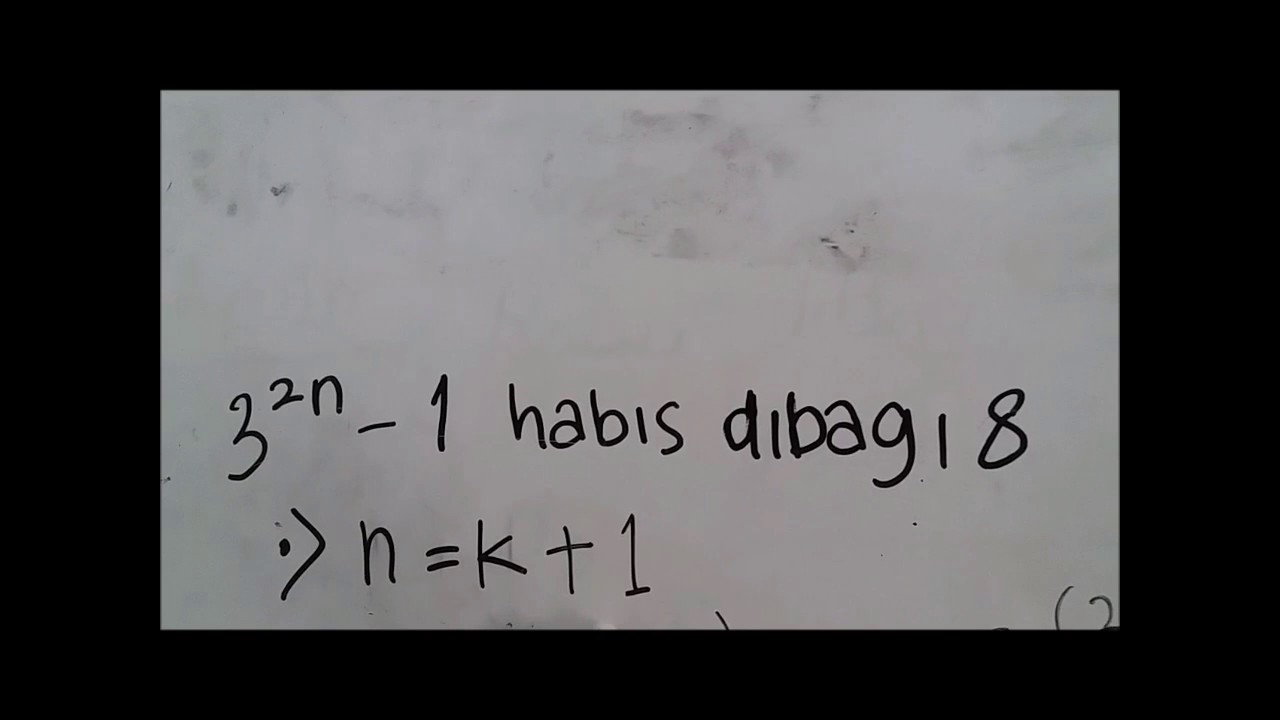
Contoh Soal Induksi Matematika Youtube

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Doc Ulangan Matematika Xii Ips Luqman Odja Academia Edu

Buktikan 4007n 1 Habis Dibagi 03 Brainly Co Id

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Soal Dan Pembahasan Suku Banyak

Induksi Matematika 4 Youtube

Rpp Kd 3 1 Induksi Matematika Fix

Kelas 11 Sma Matematika Siswa 17 Pages 1 50 Text Version Anyflip

Induksi Matematika Buktikan Bahwa 11 N 6 Habis Dibagi 5 Untuk N Bilangan Asli Youtube

Contoh Soal Induksi Matematika Habis Dibagi Brainly Kumpulan Soal Pelajaran 5

Lembar Aktivitas Siswa Matematika15 A Notasi Sigma 1 Pengertian Notasi Sigma Misalkan Jumlah Pdf Document

Rangkuman Contoh Soal Pembahasan Suku Banyak

Gunakan Induksi Matematika Untuk Menunjukan Bahwa 5n 1 Habis Dibagi 4 Untuk Semua Bilangan Bulat Brainly Co Id

Dengan Induksi Matematika 5n 3n Habis Dibagi Mas Dayat

Buktikan N N 1 N 2 Habis Dibagi 3 Induksi Matematika Bagian 6 Youtube

Dari Soal Di Bawah Ini Buktikan Bahwa 1 1 2 3 N N N 1 Adalah Benar Untuk Setiap Brainly Co Id

2 1 Pendahuluan 2 2 Keterbagian
Pdf Penyelesaian Soal Matematika Dengan Pembuktian Kusuma Hadi Purnawan Academia Edu

Soal Induksi Mtk Dan Cara Penyelesaian Mtk Smansa Aul

Soal Induksi

Teori Bilangan

Induksi Matematika Makalah Prinsip Dan Contoh Soal

Contoh Soal Induksi Matematika Dan Jawaban Pembahasan

Teori Bilangan

Soal Dan Pembahasan Induksi Matematika Sumber Soal Buku Siswa Matematika Sma Kurikulum 13 Defantri Com
Induksi Matematika Materi Lengkap Matematika



